Basic Concepts and Operations#

We define a complex number as an ordered pair $(x,y),(x,y\in\mathbb{R})$. Two complex numbers $(x_1,y_1),(x_2,y_2)$ are said to be equal if and only if $x_1=x_2$ and $y_1=y_2$. We usually use $z$ to represent a complex number.
Next, we define two operations for complex numbers.

• Addition: $(x_1,y_1)+(x_2,y_2)=(x_1+x_2,y_1+y_2)$.
• Multiplication: $(x_1,y_1)\times(x_2,y_2)=(x_1x_2-y_1y_2,x_1y_2+x_2y_1)$.

It can be easily proven that the complex numbers form a field with respect to these two operations. We call this field the Complex Number Field and denote it as $\mathbb{C}$.
Based on these operations, we define two elements: $1=(1,0),i=(0,1)$. Then we can express any complex number as:

We call $x$ the real part of $z$ and $y$ the imaginary part of $z$, denoted as:

Usually, we omit the $1$, just like in the real number field, giving complex numbers the form seen in the compulsory curriculum, and we can also obtain:

Note that $1,i$ are linearly independent. Therefore, we can use these two vectors as basis vectors to form a two-dimensional space, called the Complex Plane, as shown in the figure below:

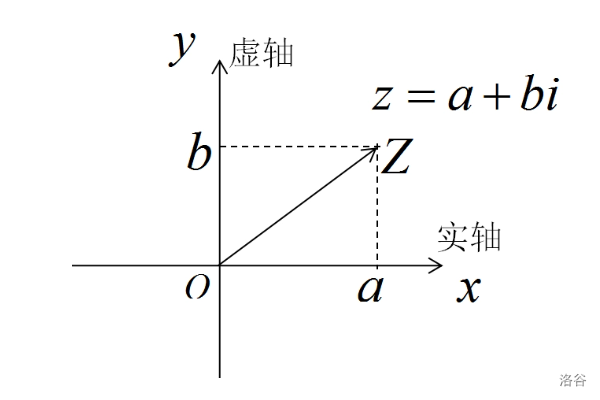
As shown, each complex number corresponds to a vector in the complex plane. The modulus of a complex number is defined as the magnitude of the corresponding vector, denoted as:

Its argument is defined as the angle of the corresponding vector, denoted as:

A vector has a trigonometric representation, so the corresponding complex number also has a trigonometric representation. Let $r=|z|,\theta=\arg(z)$, then

Complex numbers have more relations than vectors. For example, we say two complex numbers $z_1=(x_1,y_1),z_2=(x_2,y_2)$ are

• conjugates if $x_1=x_2,y_1=-y_2$, denoted as $z_1=\overline{z_2}$.

It is easy to see that the Completeness Axiom does not hold in the complex number field; that is, the complex numbers are not an ordered field. We can map points on the complex plane to a sphere (Riemann sphere), but I’m too lazy to write about that. If you want to learn more, you can read Shabat’s “Introduction to Complex Analysis”.

A complex function $w:\mathbb{C}\to\mathbb{C}$ is a rule defined on the complex field that maps to the complex plane. Generally, a complex function can be split into two real functions defined on the complex field, like:

where $x,y,u(x,y),v(x,y)\in\mathbb{R}$.

Exponential Function#

We consider defining it similarly to the real number field:

Then we consider whether this limit exists.
We note that:

Thus, this limit exists, and we have:

Setting $x=0$, we obtain Euler’s formula. From now on, I will treat it as a known result in the subsequent sections.

Power Function#

With Euler’s formula, a complex number can be represented as:

This is a more concise form. This form is beneficial as it makes the power function more intuitive. Consider $z=r e^{i\theta}$, then

This means the argument is multiplied by $n$, and the modulus is raised to the $n$th power, making the geometric interpretation more intuitive.

Trigonometric Functions, Hyperbolic Functions#

With Euler’s formula, trigonometric functions can also be expressed using it:

Notice how this looks just like the hyperbolic functions? So we can get the following expressions:

Then we can define the remaining functions using $\sin,\cos,\sinh,\cosh$.

Derivative#

In the pure real number field, the derivative is usually represented as a rate of change. But does this hold in the complex field? In other words, do derivatives exist in the complex field? If they do, what are the conditions for existence?

We define the derivative of a complex function similarly to the real case:

It seems the same as the real case! But a problem arises here: from which direction should $z$ approach $z_0$?

Here we give the Cauchy-Riemann conditions: This function is differentiable (complex differentiable) if and only if:

Then, at that point, $w'=\frac{\partial u}{\partial x}+i\frac{\partial v}{\partial x}$. The proof is straightforward.
If a function is differentiable at every point in its domain, it is called a holomorphic function. From now on, the functions we discuss will be holomorphic functions.

Integral#

In the complex field, integration is defined along paths, generally called line integrals or contour integrals.

Let a path be defined by $\gamma=\gamma(t)=x(t)+i\cdot y(t),t\in[a,b]$. Then the integral is defined as:

Based on this definition, we can derive the following simple properties:

• Path Additivity: If $\gamma=\gamma_1+\gamma_2$, then: $\int_\gamma f(z)\,dz=\int_{\gamma_1} f(z)\,dz+\int_{\gamma_2} f(z)\,dz$
• Reverse Path: For any path, we have: $\int_{-\gamma} f(z)\,dz=-\int_\gamma f(z)\,dz$

Cauchy’s Theorem#

Simply Connected Region: In Shabat’s Introduction to Complex Analysis, homotopy theory of paths is used to rigorously define a simply connected region. However, the author’s language skills are poor and unable to articulate a rigorous definition clearly, coupled with the inherently high difficulty of understanding, so we define a simply connected region in an easy-to-understand way here.

If a region has no “holes” in it, it is called a simply connected region. Otherwise, it is called a multiply connected region.

Do simply connected regions have any magical properties? Certainly, otherwise I wouldn’t have mentioned them specifically.

Theorem 1: If $f(z)$ is holomorphic in a simply connected region $D$, then for any closed curve $\gamma\subset D$, we always have:

(The circle on the integral sign indicates integration over a closed curve).
This theorem essentially tells us that for integrals in a simply connected region, the value of the integral depends only on the start and end points, and is independent of the path. This is a very strong conclusion. It directly tells us that within a simply connected region, we only need to consider the start and end points, greatly simplifying the complexity of calculation. For example, we can transform a bizarre integration path into a straight line segment, and the integral over a line segment is just an ordinary integral~

Theorem 2: If $z_0$ is inside the closed curve $\gamma$, then:

This is an extremely important theorem. It allows us to convert many integrals into function values, and function values into contour integrals.

Relationship Between Higher-Order Derivatives and Integrals#

This is a particularly important part, so I’ve dedicated a separate section to explain it.

There exists the following relationship between the higher-order derivatives of a function and integrals:

We prove this using mathematical induction.

Proof

When $n=0$, it reduces to Cauchy’s Integral Formula (Theorem 2), so the proposition holds. If the proposition holds for $n=k$, then:

We differentiate this with respect to $z_0$:

Therefore, the proposition holds for $\forall n\in\mathbb{N}$.

We will use this in the Taylor expansion in the complex domain.

Taylor Series#

Let’s recall the Cauchy Integral Formula derived earlier:

We consider expanding its kernel. Using a known result (geometric series), we get:

Substituting back into the original formula, we get:

Does the latter part look familiar? This is the higher-order derivative formula we just derived. Substituting it in, we obtain:

This is the same result we obtained in the pure real number domain! But it’s not over yet; we still need to discuss the convergence conditions for the Taylor series.

Obviously, the methods we used for expanding real functions are no longer applicable here. So we present a better method here.

Cauchy–Hadamard Theorem#

This is a superior method for determining convergence, giving a radius of convergence.

Cauchy–Hadamard Theorem: For the series $\displaystyle\sum_{n=0}^\infty c_n(z-z_0)^n$, its radius of convergence $R$ satisfies the following relation:

Specifically, we define:

• $R=\infty$ when $\frac1R=0$.
• $R=0$ when $\frac1R=\infty$.

Proof

Here we only prove the case for $z_0=0$, as other cases can be obtained by substitution.
Let $L=\displaystyle\varlimsup_{n\to\infty}\sqrt[n]{|c_n|}$. Consider calculating:

Let’s discuss case by case:

1. $|z|\cdot L=0$, then clearly, for any $z$ in the complex plane, the series converges.
2. $|z|\cdot L\in(0,1)$ i.e. $|z|<\frac1L$, then the series converges absolutely.
3. $|z|\cdot L=1$ the test is inconclusive.
4. $|z|\cdot L\in(1,\infty)$, i.e. $|z|>\frac1L$, then the series diverges, because $|c_nz^n|>1$ for infinitely many $n$.
5. $|z|\cdot L=\infty$ then the series converges only for $z=0$.

In summary, except for the boundary case, the proposition holds.

Laurent Series#

Starting from here, we will discuss functions that are not holomorphic everywhere due to the presence of singularities.

Assume the function $f(z)$ is holomorphic on the annulus $r\le|z-z_0|\le R$. Then there exists a series:

where

and where $r\le\rho\le R$. We call this series the Laurent series.

We find that when $0\le n$, the coefficients of the series are the same as those in the Taylor series, but they cannot be written in the form $c_n=\frac{f^{(n)}(z_0)}{n!}$ if $f$ is not analytic at $z_0$.

Its convergence can also be determined using the Cauchy–Hadamard theorem. Furthermore, its coefficients satisfy Cauchy’s inequality:

where $M\ge\sup(f)$.

Fourier Series#

Recall the definition of the Fourier series in the real number domain:

where:

Applying Euler’s formula mentioned earlier and defining new coefficients, we can write:

A simple derivation yields:

Note that if we let $z=e^{int}$ we get:

and

This is the Laurent series on the unit circle. Conversely, the Laurent series of a function on the unit circle can be transformed into a Fourier series by substitution.

Isolated Singularities#

We define a point $z_0$ as an isolated singularity of the function $f$ if $f$ is holomorphic in the punctured disk $0<|z-z_0|<r$ for some $r>0$.

We say the isolated singularity $z_0$ is:

• A removable singularity if the limit $\displaystyle\lim_{z\to z_0} f(z)=A$ exists (and is finite).
• A pole if the limit $\displaystyle\lim_{z\to z_0}f(z)=\infty$.
• An essential singularity if the limit $\displaystyle\lim_{z\to z_0}f(z)$ does not exist (in the extended complex plane).

This passage probably has the distinctive inverted flavor of foreign textbooks. Would it sound more like it if the top part was written as: “Regarding an isolated singularity $z_0$, we call it…”?

Here are two examples. For the functions:

Clearly $z_0=0$ is a removable singularity for $f_1$ and an essential singularity for $f_2$.

Theorem 3: $z_0$ is a removable singularity of the function $f$ if and only if the coefficients $c_n$ in the Laurent series of $f$ about $z_0$ satisfy:

The reader is invited to prove this themselves; you can try using Cauchy’s inequality.

Theorem 4: $z_0$ is a pole of the function $f$ if and only if the coefficients $c_n$ in the Laurent series of $f$ about $z_0$ satisfy: There exists an integer $N<0$ such that $c_n=0$ for all $n\le N$. The reader is invited to prove this again.

Theorem 4’: $z_0$ is a pole of the function $f$ if and only if the function $\varphi=\frac1f$ is holomorphic in a neighborhood of $z_0$ and has $\varphi(z_0)=0$.

Theorem 5: $z_0$ is an essential singularity of the function $f$ if and only if the coefficients $c_n$ in the Laurent series of $f$ about $z_0$ satisfy: There are infinitely many negative indices $n$ for which $c_n\ne0$.

From Theorems $3$ to $5$, we can see the relationship between isolated singularities and the Laurent series.

Residue Theorem#

We now start considering points where a holomorphic function is no longer holomorphic.

Assume the function $f$ is holomorphic everywhere in a region $D$ except at a countable set of singular points. Let region $G\subseteq D$, and let $a_1,\cdots,a_n$ be the singularities inside $G$. Let $\gamma_\nu=\{|z-a_\nu|=r\}$, where $r$ is sufficiently small such that the disks around the singularities do not intersect. Let $\gamma_\nu$ be oriented counterclockwise. Define $G_r=G\setminus \bigcup _{\nu=1}^n \text{interior of } \gamma_\nu$.

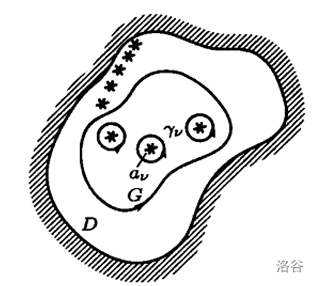
The diagrams in complex analysis are great.

Then we clearly have (by Cauchy’s Theorem for multiply connected domains, applying it to $G_r$):

We define $\mathrm{res}_\nu f=\displaystyle\frac{1}{2\pi i}\int_{\gamma_\nu}f(z)\,dz$, called the residue of $f$ at the singularity $a_ν$. Then the original equation becomes:

Then the Residue Theorem states: The residue of a function $f$ at an isolated singularity $a\in D$ is the coefficient $c_{-1}$ in the Laurent series expansion of $f$ about $a$, i.e.:

The proof is overly obvious. The reader can easily prove it themselves.

Here is a classic example of using residues to compute an integral. Consider computing the Laplace integral:

First, construct a closed contour representing a semicircle of radius $R>b$, denoted $\gamma$, like this:

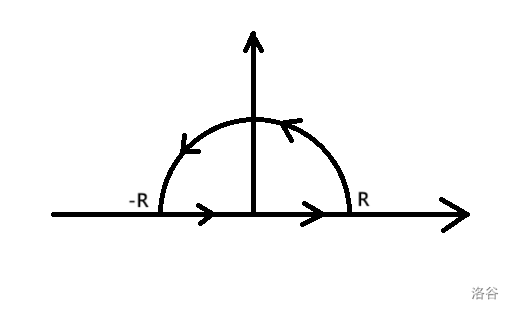
Considering the integral along this path:

There is a first-order pole (simple pole) at $z=ib$ (in the upper half-plane). Applying the residue theorem, we get:

Thus, by the residue theorem:

According to the preceding properties, we split it into two parts:

Now we let $R\to\infty$. The first part becomes the Laplace integral. For the second part, we have:

But this only holds for $a > 0$. So when $a < 0$, we take the lower semicircle as the contour integral. Using the same method, we eventually get:

Combining the two results, we get: